سیالات محاسباتی
۱. تعریف سیالات محاسباتی
سیالات محاسباتی (CFD) شاخهای از مهندسی و فیزیک محاسباتی است که رفتار جریان سیال و انتقال حرارت و جرم را با استفاده از مدلهای ریاضی و شبیهسازیهای کامپیوتری مطالعه میکند.
به جای اینکه فقط آزمایشگاهی سیالات و سیالات محاسباتی را بررسی کنیم، CFD این امکان را میدهد که پدیدهها را روی کامپیوتر شبیهسازی کنیم و نتایج را پیشبینی کنیم.
2. کاربردهای CFD سیالات محاسباتی
CFD در صنایع مختلف کاربرد دارد، از جمله:
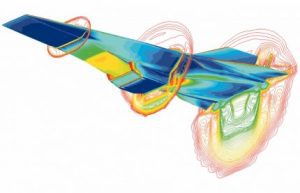
هوافضا: طراحی بال هواپیما، پیشبینی جریان هوا
خودرو: بهینهسازی آیرودینامیک خودرو
مهندسی شیمی: طراحی راکتور، مخازن اختلاط
مهندسی مکانیک: سیستمهای تهویه، توربینها
محیط زیست: پیشبینی حرکت آب در رودخانهها و اقیانوسها
3. مراحل حل مسائل CFD
مدلسازی فیزیکی: مشخص کردن جریان، سیال، هندسه و شرایط مرزی
معادلات حاکم : استفاده از معادلات ناویر-استوکس (Navier-Stokes) و قانون بقای جرم و انرژی
شبکهبندی (Meshing) سیالات محاسباتی: تقسیم محیط به شبکهای از حجمهای کوچک
حل عددی سیالات محاسباتی: حل معادلات با روشهای عددی (مثل روش حجم محدود یا المان محدود)
تحلیل نتایج سیالات محاسباتی: بررسی سرعت، فشار، دما، و سایر پارامترها
4. مزایای CFD سیالات محاسباتی
کاهش هزینه و زمان نسبت به آزمایشهای فیزیکی
امکان بررسی شرایطی که در آزمایشگاه سخت یا غیرممکن هستند
امکان بهینهسازی سریع طراحیها
5. معادلات اصلی در CFD
معادلاتی که CFD بر اساس آنها کار میکند، معادلات حاکم سیالات هستند، از جمله:
-
معادله بقای جرم (Continuity Equation)
این معادله بیان میکند که جرم سیال در طول زمان حفظ میشود. برای سیال تراکمپذیر و تراکمناپذیر شکل متفاوتی دارد.برای سیال تراکمناپذیر:
∇⋅v⃗=0\nabla \cdot \vec{v} = 0∇⋅v=۰
که v⃗\vec{v}v سرعت جریان است.
-
معادلات ناویر-استوکس (Navier-Stokes Equations)
اینها معادلات حرکت سیال هستند و شامل اثرات اینرسی، فشار، ویسکوزیته و نیروهای خارجی میشوند:ρ(∂v⃗∂t+v⃗⋅∇v⃗)=−∇p+μ∇2v⃗+F⃗\rho \left( \frac{\partial \vec{v}}{\partial t} + \vec{v} \cdot \nabla \vec{v} \right) = -\nabla p + \mu \nabla^2 \vec{v} + \vec{F}ρ(∂t∂v+v⋅∇v)=−∇p+μ∇۲v+F
ρ\rhoρ: چگالی
ppp: فشار
μ\muμ: ویسکوزیته
F⃗\vec{F}F: نیروهای خارجی
-
معادله انرژی (Energy Equation) سیالات محاسباتی
برای مسائل انتقال حرارت یا جریان با تغییر دما استفاده میشود:ρcp(∂T∂t+v⃗⋅∇T)=k∇2T+S\rho c_p \left( \frac{\partial T}{\partial t} + \vec{v} \cdot \nabla T \right) = k \nabla^2 T + Sρcp(∂t∂T+v⋅∇T)=k∇۲T+S
که TTT دما، cpc_pcp ظرفیت گرمایی و kkk ضریب هدایت حرارتی است.
6. شبکهبندی (Meshing) سیالات محاسباتی
برای شبیهسازی، محیط مورد نظر به شبکهای از سلولهای کوچک تقسیم میشود.
هر سلول مقدار فشار، سرعت و دما دارد.
هرچه شبکه ریزتر باشد، دقت بیشتر ولی زمان محاسبات طولانیتر.
انواع شبکه: ساختاری (Structured) و غیرساختاری (Unstructured).
7. روشهای عددی (Numerical Methods) سیالات محاسباتی
برای حل معادلات بالا به صورت عددی از روشهای مختلف استفاده میشود:
Finite Difference Method (FDM) – روش تفاضل محدود
Finite Volume Method (FVM) – روش حجم محدود
Finite Element Method (FEM) – روش المان محدود
روش FVM در CFD رایجترین است، چون حفظ جرم و انرژی در هر سلول شبکه را تضمین میکند.
۸. تحلیل نتایج
بعد از شبیهسازی، نتایج به شکل:
نقشه سرعت (Velocity Field)
نقشه فشار (Pressure Field)
نقشه دما (Temperature Field)
نمایش داده میشوند و میتوان جریانهای پیچیده، توربولانس و نقاط بحرانی را مشاهده کرد.
۹. چالشها و محدودیتها
جریانهای توربولانسی پیچیده نیاز به مدلهای پیشرفته دارند.
زمان محاسباتی زیاد برای شبکههای ریز.
خطاهای ناشی از تقریبی بودن روش عددی و فرضیات مدل.
